martes, 28 de diciembre de 2010
martes, 23 de noviembre de 2010
Karl Popper
K. R. Popper nace en Viena. Después de estudiar filosofía se traslada a Londres, donde desde 1945 enseña en la Universidad de Londres. Sus Trabajos más importantes se centran en el campo de la Teoría de las ciencia como principal representante del Racionalismo Crítico en contra de cualquier otra utopía social revolucionaria: contra la revolución Popper propone la razón o la reforma gradual. La idea fundamental de la epistemología popperiana gira en torno al principio de la falsificación, o sea, la demostración del error. Este principio nos da el criterio popperiano de demacración entre teorías empíricas (científicas) y no empíricas. El método científico, que según Popper es único en todo campo de investigaciín científica, se desarrolla en forma de triada: - Problema
- Conjetura
- Refutación.
Esto es lo que Popper Escribe en su obra Lógica de la investigación científica.
solo escribiré algunos fragmentos de la primera parte que trata de Panoramas de Algunos y problemas Fundamentales del problema de la indicción.
Panoramas de Algunos problemas Fundamentales
El hombre de ciencia, ya sea teórico o experimental, propone enunciados (o sistemas de enunciados) y los contrasta paso a paso. En particular, en el campo de las ciencias empíricas construye hipótesis o sistemas de teorias y las contrasta con la experiencia por medio de observaciones y experimentos.
Según mi opinión, la tarea de la lógica de la investigación científica (o lógica del conocimiento) es ofrecer un análisis lógico de tal modo de proceder: esto es , analizar el método de las ciencias empíricas.
1.El problema de la inducción.
Se conoce con el nombre del problema de la inducción la cuestión acerca de si están justificadas las inferencias inductivas, o de bajo qué condiciones están.
El problema de la inducción puede formularse a asimismo, como la cuestión sobre como establecer la verdad de los enunciados universales basados en la experiencia (como son la hipótesis y los sistemas teóricos de las ciencias empíricas). Pues muchos creen que la verdad de estos enunciados se sabe por experiencia; sin embargo, es claro que todo informe en que se da cuenta de una experiencia o de una observación o del resultado de un experimento, no puede ser originalmente un enunciado universal, sino un enunciado singular. Por lo tanto, quien dice que sabemos por experiencia la verdad de un enunciado universal suele querer decir que la verdad de dicho enunciado puede reducirse , de cierta forma a la verdad de otros enunciados singulares que son verdaderos según sabemos por la experiencia; lo cual equivale a decir que los enunciados universales está basados en inferencias inductivas. Así pues, la pregunta acerca de si hay leyes naturales cuya verdad nos conste viene a ser otro modo de preguntar si las inferencias inductivas están justificadas lógicamente.
La importancia de un principio de inducción para el método científico es máxima: Este principio dice Reichenbach determina la verdad de las teorías científicas; eliminarlo de la ciencia significaría nada menos que privar a esta de la posibilidad de decidir sobre la verdad o falsedad de sus teorías; es evidente que sin el la ciencia perdería el derecho de distinguir sus teorías de las creaciones fantásticas y arbitrarias de la imaginación del poeta.
Pero tal principio de inducción no puede ser una verdad puramente lógica , si existiera un principio de inducción puramente lógico no habría problema de la inducción......
En este capitulo Popper analiza el trabajo del hombre de ciencia y problemas teorético-cognoscitivos como el problema de la inducción.
Yo coincido con su idea de que La ciencia o el conocimiento empírico ha de progresar mediante la falsificación de sus enunciados. La falsificación consiste, en pocas palabras, en la demostración del error y no en la verificación o confirmación.
Estos son algunas obras de Popper:
La Lógica de la investigación científica.
Conocimiento científico
El desarrollo del conocimiento científico. Conjeturas y demostraciones
La miseria del historicismo
La sociedad abierta y sus enemigos
A mi no me gusta copiar y pegar así que escribí lo que recuerdo haber leído antes acerca de Popper espero que este bien.
INDUCCIÓN MATEMÁTICA
A manera de introducción hacia el estudio de la inducción matemática, anotaré los postulados o axiomas de Peano que nos servirán para poder realizar demostraciones con éste recurso, la inducción matemática.
Los cinco axiomas siguientes conocidos como postulados de Peano por el
matemático italiano que los enuncio en 1899, se pueden establecer como
sigue:
1. 1 es un número natural. (es decir, el conjunto de los números naturales no es vacío)
2. Si a es un número natural, entonces a+1 también es un número natural (llamado el sucesor de a).
3. 1 no es sucesor de ningún número natural. (primer elemento del conjunto)
4. Si hay dos números naturales a y b tales que sus sucesores son diferentes entonces a y b son números naturales diferentes.
5. Axioma de inducción: si un conjunto de números naturales contiene al 1 y a los sucesores de cada uno de sus elementos entonces contiene a todos los números naturales.
Conociendo los axiomas de Peano particularmente el quinto podemos dar paso a lo que es la demostración por inducción matemática, finalizando con algunas notas que serán de utilidad al hacer la demostración.
*DEMOSTRACIÓN POR INDUCCIÓN MATEMÁTICA
El quinto postulado de Peano nos indica que siempre es posible alcanzar un número natural
“n” teniendo como punto de partida al número uno y recorriendo los siguientes uno a uno
hasta llegar al número natural “n”. Este postulado, también es conocido con frecuencia
como “principio de inducción”, es la base del método de demostración conocido como
inducción matemática.
El proceso de una demostración por inducción matemática consiste de los siguientes pasos:
1) Escribir claramente la proposición P(n) cuya validez quiere demostrase, especificando la
variable de inducción y el conjunto de valores que puede asignarse a dicha variable. Por
ejemplo, si se escribe P(n), n representa la variable de inducción; si se escribe P(m), m
es la variable de inducción, en general la letra contenida en el paréntesis de P( ), denota
la variable de inducción.
2) Si P(n) es una proposición enunciada para todos los números naturales, se debe verificar
el cumplimiento de la proposición para el menor valor de n (esto equivale a verificar
que 1 pertenece a S, según el quinto postulado de Peano, esto es, verificar que la
proposición se cumple para cuando n =1).
3) Si el punto i se cumple, entonces planteamos que P(k) también se cumple, esto será
nuestra hipótesis, a partir de ello planteamos que para el siguiente de k también se
cumplirá P(k+1) esta será nuestra tesis que debemos demostrar que es verdadera (esto
equivale a demostrar que si k pertenece a S entonces k+1 pertenece a S de acuerdo con
el quinto postulado de Peano).
4) Cuando demostramos la validez de la tesis, se concluye que P(n) es verdadera para todo
n en el conjunto de los números naturales. TIP: Una forma de demostrar la validez de la
tesis es partiendo de la hipótesis.
NOTA: Las primeras preguntas que debemos hacernos al inicio de cada ejercicio son:
¿Cuál es la proposición P(n) cuya validez desea demostrarse?
¿Cuál es la variable de inducción?
¿En que conjunto ha sido enunciada dicha proposición?
NOTA CULTURAL
Al inicio hablamos de los postulados de Peano pero poco conocemos sobre ese personaje,así que en ésta parte de la publicación anotaré algunos datos biográficos que servirán para la formación cultural.
Giuseppe Peano
(Cuneo, actual Italia, 1858-Turín, 1932) Matemático italiano. Estudió en la Universidad de Turín, ciudad a la que su familia se había trasladado en 1870. Sus aportaciones más recordadas son las referentes a la axiomática de las matemáticas. A ese respecto cabe destacar su sus axiomas sobre el conjunto de los números enteros naturales o sobre la estructura de un espacio vectorial, así como la definición del concepto de aplicación lineal. Interesado en el uso de la lógica más como medio de exposición de la matemática que como su fundamento (al estilo de Frege o Russell), desarrolló una sintaxis muchos de cuyos símbolos (como los de pertenencia, unión o intersección) son hoy día empleados de forma universal. En su constante empeño de expulsar la ambigüedad del ámbito de las definiciones y los teoremas matemáticos, tuvo por costumbre denunciar las incorrecciones presentes en la obra tanto de sus predecesores como de sus contemporáneos; se convirtió así en un especialista del contraejemplo, el más famoso de los cuales fue la redefinición del concepto de curva anteriormente propuesto por Camille Jordan.
Los cinco axiomas siguientes conocidos como postulados de Peano por el
matemático italiano que los enuncio en 1899, se pueden establecer como
sigue:
1. 1 es un número natural. (es decir, el conjunto de los números naturales no es vacío)
2. Si a es un número natural, entonces a+1 también es un número natural (llamado el sucesor de a).
3. 1 no es sucesor de ningún número natural. (primer elemento del conjunto)
4. Si hay dos números naturales a y b tales que sus sucesores son diferentes entonces a y b son números naturales diferentes.
5. Axioma de inducción: si un conjunto de números naturales contiene al 1 y a los sucesores de cada uno de sus elementos entonces contiene a todos los números naturales.
Conociendo los axiomas de Peano particularmente el quinto podemos dar paso a lo que es la demostración por inducción matemática, finalizando con algunas notas que serán de utilidad al hacer la demostración.
*DEMOSTRACIÓN POR INDUCCIÓN MATEMÁTICA
El quinto postulado de Peano nos indica que siempre es posible alcanzar un número natural
“n” teniendo como punto de partida al número uno y recorriendo los siguientes uno a uno
hasta llegar al número natural “n”. Este postulado, también es conocido con frecuencia
como “principio de inducción”, es la base del método de demostración conocido como
inducción matemática.
El proceso de una demostración por inducción matemática consiste de los siguientes pasos:
1) Escribir claramente la proposición P(n) cuya validez quiere demostrase, especificando la
variable de inducción y el conjunto de valores que puede asignarse a dicha variable. Por
ejemplo, si se escribe P(n), n representa la variable de inducción; si se escribe P(m), m
es la variable de inducción, en general la letra contenida en el paréntesis de P( ), denota
la variable de inducción.
2) Si P(n) es una proposición enunciada para todos los números naturales, se debe verificar
el cumplimiento de la proposición para el menor valor de n (esto equivale a verificar
que 1 pertenece a S, según el quinto postulado de Peano, esto es, verificar que la
proposición se cumple para cuando n =1).
3) Si el punto i se cumple, entonces planteamos que P(k) también se cumple, esto será
nuestra hipótesis, a partir de ello planteamos que para el siguiente de k también se
cumplirá P(k+1) esta será nuestra tesis que debemos demostrar que es verdadera (esto
equivale a demostrar que si k pertenece a S entonces k+1 pertenece a S de acuerdo con
el quinto postulado de Peano).
4) Cuando demostramos la validez de la tesis, se concluye que P(n) es verdadera para todo
n en el conjunto de los números naturales. TIP: Una forma de demostrar la validez de la
tesis es partiendo de la hipótesis.
NOTA: Las primeras preguntas que debemos hacernos al inicio de cada ejercicio son:
¿Cuál es la proposición P(n) cuya validez desea demostrarse?
¿Cuál es la variable de inducción?
¿En que conjunto ha sido enunciada dicha proposición?
NOTA CULTURAL
Al inicio hablamos de los postulados de Peano pero poco conocemos sobre ese personaje,así que en ésta parte de la publicación anotaré algunos datos biográficos que servirán para la formación cultural.
Giuseppe Peano
(Cuneo, actual Italia, 1858-Turín, 1932) Matemático italiano. Estudió en la Universidad de Turín, ciudad a la que su familia se había trasladado en 1870. Sus aportaciones más recordadas son las referentes a la axiomática de las matemáticas. A ese respecto cabe destacar su sus axiomas sobre el conjunto de los números enteros naturales o sobre la estructura de un espacio vectorial, así como la definición del concepto de aplicación lineal. Interesado en el uso de la lógica más como medio de exposición de la matemática que como su fundamento (al estilo de Frege o Russell), desarrolló una sintaxis muchos de cuyos símbolos (como los de pertenencia, unión o intersección) son hoy día empleados de forma universal. En su constante empeño de expulsar la ambigüedad del ámbito de las definiciones y los teoremas matemáticos, tuvo por costumbre denunciar las incorrecciones presentes en la obra tanto de sus predecesores como de sus contemporáneos; se convirtió así en un especialista del contraejemplo, el más famoso de los cuales fue la redefinición del concepto de curva anteriormente propuesto por Camille Jordan.
sábado, 13 de noviembre de 2010
Caída Libre
Hasta el siglo XVI se aceptaba la concepción que tuvo Aristoteles acerca de la caída libre el afirmaba que los objetos pesados caían más rápido que los ligeros.
Galileo Galilei refutó la concepción de Aristótelica al afirmar que, en ausencia de resistencia de aire, todos los objetos caen con una misma aceleración uniforme.Probó su hipótesis usando planos inclinados, con lo que conseguía un movimiento más lento, el que podía medir usando su pulso como reloj. Al incrementar de manera gradual la pendiente del plano dedujo conclusiones acerca de objetos que caían libremente.
Cuando se emplea el término objeto en caída libre se incluye tanto el soltar como el lanzar hacia arriba o hacia abajo el objeto. Cualquier objeto que cae libremente tiene una aceleración dirigida hacia abajo, independientemente del movimiento inicial del objeto. La magnitud de esta aceleración
de caída libre se denota con el símbolo g, cuyo valor varía ligeramente con la altura y con la latitud. En la cercanía de la superficie de la Tierra el valor de g es aproximadamente $9.8 m/s^2$.
La causa de esta aceleración fue encontrada por Newton,quien estableció en su ley de Gravitación Universal que las masas se atraen en proporción directa al producto de sus masas e inversamente a su separación al cuadrado. Es la masa de la Tierra la que origina esta aceleración de $9.8 m/s^2$ en su superficie.
La caída libre es un ejemplo común de movimiento uniformemente acelerado, con una aceleración
$a = -9,8 m/s^2$.
Ejemplo de caída libre sin fricción de un cuerpo:Caída Libre
Galileo Galilei refutó la concepción de Aristótelica al afirmar que, en ausencia de resistencia de aire, todos los objetos caen con una misma aceleración uniforme.Probó su hipótesis usando planos inclinados, con lo que conseguía un movimiento más lento, el que podía medir usando su pulso como reloj. Al incrementar de manera gradual la pendiente del plano dedujo conclusiones acerca de objetos que caían libremente.
Cuando se emplea el término objeto en caída libre se incluye tanto el soltar como el lanzar hacia arriba o hacia abajo el objeto. Cualquier objeto que cae libremente tiene una aceleración dirigida hacia abajo, independientemente del movimiento inicial del objeto. La magnitud de esta aceleración
de caída libre se denota con el símbolo g, cuyo valor varía ligeramente con la altura y con la latitud. En la cercanía de la superficie de la Tierra el valor de g es aproximadamente $9.8 m/s^2$.
La causa de esta aceleración fue encontrada por Newton,quien estableció en su ley de Gravitación Universal que las masas se atraen en proporción directa al producto de sus masas e inversamente a su separación al cuadrado. Es la masa de la Tierra la que origina esta aceleración de $9.8 m/s^2$ en su superficie.
La caída libre es un ejemplo común de movimiento uniformemente acelerado, con una aceleración
$a = -9,8 m/s^2$.
Ejemplo de caída libre sin fricción de un cuerpo:Caída Libre
Ejemplo de la página 76 del libro de Polya
Construir un triángulo dados un lado $a$ la altura $h$ perpendicular a $a$ y el ángulo $\alpha$
Datos:
Un elemento $h$ un ángulo $\alpha$ y dos puntos $B$ y $C$ cuyas posiciones son dadas.
La perpendicular del punto $A$ al segmento $BC$ debe ser igual a $h$, y el $\angle{BCA}=\alpha$
Distinguir las nuevas partes de la condición.
La condición consta de dos partes, una concerniente al lado $h$, la otra al dato $\alpha$.
El punto que desconocemos debe cumplir:
1). Estar situado a una distancia $h$ del segmento $BC$.
2). Ser el vértice de un ángulo de una amplitud dada $\alpha$, cuyos lados contengan a los puntos $B$ y $C$.
Hay numerosos puntos que satisfacen la parte 1) de la condición, a saber, todos los puntos de una paralela a la línea $BC$ a la distancia $h$ de dicho segmento. Esta paralela es el lugar geométrico de los puntos que satisfacen la parte 1) de la condición. El lugar geométrico de los puntos que satisfacen la parte 2) es un cierto arco de circunferencia cuyos puntos extremos son $B$ y $C$. Determinando esos dos lugares geométricos, sabemos que su intersección es el punto que deseamos determinar.
Datos:
Un elemento $h$ un ángulo $\alpha$ y dos puntos $B$ y $C$ cuyas posiciones son dadas.
La perpendicular del punto $A$ al segmento $BC$ debe ser igual a $h$, y el $\angle{BCA}=\alpha$
Distinguir las nuevas partes de la condición.
La condición consta de dos partes, una concerniente al lado $h$, la otra al dato $\alpha$.
El punto que desconocemos debe cumplir:
1). Estar situado a una distancia $h$ del segmento $BC$.
2). Ser el vértice de un ángulo de una amplitud dada $\alpha$, cuyos lados contengan a los puntos $B$ y $C$.
Hay numerosos puntos que satisfacen la parte 1) de la condición, a saber, todos los puntos de una paralela a la línea $BC$ a la distancia $h$ de dicho segmento. Esta paralela es el lugar geométrico de los puntos que satisfacen la parte 1) de la condición. El lugar geométrico de los puntos que satisfacen la parte 2) es un cierto arco de circunferencia cuyos puntos extremos son $B$ y $C$. Determinando esos dos lugares geométricos, sabemos que su intersección es el punto que deseamos determinar.
Ejemplo de la página 68 del libro de Polya.
Determinar el punto de intersección de un recta dada y una parábola; cuyo foco y directriz son dadas.
$\LaTeX$
Datos:
Sabemos las coordenadas de los puntos.
P(x,y)
q(x,0)
F(o,f)
Vértice(0,f/2)
Ecuación de la parábola
$ x^2 = 4py $
$x=2\sqrt{py}$
$y=mx+b$
$x^2=4(x,y)$
$Pq=Fq$
$Pq = \sqrt{(x2-x1)^2+(y-y)^2}$
$Pq=\sqrt{x_2^2-2x_2x_1+x^2+y^2}$
$F=(0,f)$ $q=(x,y)$
$FP=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
$FP=\sqrt{(x-0)^2+(y-f)^2}$
$FP^2=x^2+(y-f)^2$
$FP^2=x^2+y^2-2fy+f^2$
$FP^2=x^2+y^2-2f(mx+b)+f^2$
$x^2+y^2-2fmx-2fb+f^2$
$0=x^2-2fmx-2fb+f^2$
Completando cuadrados
$(x-fm)^2=2fb-f^2+fm^2$
$x-fm=\sqrt{2fb-f^2+fm^2}$
$x=fm+\sqrt{2fb-f^2+fm^2}$
$x=fm+\sqrt{f(2b+(m-1)f)}$
Divisiones Principales, Preguntas Principales.
Ejemplo de la página 29 del libro de Polya.
Determinar la diagonal de un paralelepípedo rectangular dados su longitud, su ancho y su altura.
Determinar la diagonal de un paralelepípedo rectangular dados su longitud, su ancho y su altura.
Premio Nobel de Física 2010
Los físicos rusos Andre Geim y Konstantin Novoselov ganaron el Premio Nobel De Física, por sus trabajos pioneros en el desarrollo del grafeno, un material bidimensional útil para crear dispositivos electrónicos flexibles y más eficientes, como ordenadores y pantallas táctiles así como paneles solares.
Geim, de 51 años, y Novoselov, de 36, recibirán el premio de la Academia sueca el próximo 10 de diciembre por sus experimentos con este nuevo material, que posibilita avances decisivos en la Física cuántica.
Los dos son rusos de nacimiento y actualmente investigan en la Universidad de Manchester (Reino Unido). Geim, nacido en Sochi, Rusia, en 1958 y nacionalizado holandés, se doctoró en Ciencias Físicas en 1987 en la Academia Rusa de Ciencias de Chernogolovka.
¿Qué es el Grafeno?
El grafeno es una estructura laminar plana, de un átomo de grosor, compuesta por átomos de carbono densamente empaquetados en una red cristalina en forma de panal de abeja.
Los premiados obtuvieron el grafeno a partir del grafito (usado para fabricar lápices). Este nuevo material se caracteriza por poseer una alta conductividad térmica y eléctrica y por combinar una alta elasticidad y ligereza con una extrema dureza, que lo sitúa como el material más resistente del mundo.Además, puede reaccionar químicamente con otros elementos y compuestos químicos, lo que convierte al grafeno en un material con un gran potencial de desarrollo.
Demostración del Teorema de Pitágoras.
EL área del cuadrado exterior es $(x+y)^2$ y el área del cuadrado interior es $r^2$
Y el área de cada uno de los triángulos es xy/2 (recordemos que el área de un triángulo es base por altura partido por 2. Como el cuadrado exterior está formado por el cuadrado interior y los cuatro triángulos se tiene que el área de aquél es la suma de las áreas de éstos, es decir:
$(x+y)^2=r^2 + \frac{4xy}{2}$
$(x+y)^2=x^2+2xy+y^2$
igualando ambas expresiones tenemos que:
$x^2+2xy+y^2=r^2+2xy$
$x^2+y^2=r^2$
PROBLEMA DE LA PÁGINA 29 DEL LIBLO DE POLYA Y EL PROBLEMA DEL VENDEDOR
Determinar la diagonal de un paralelepípedo rectangular dados su longitud, su ancho y su altura.
Solución:
x=x(a,b,c)
Aplicando el teorema de Pitágoras tenemos que:
$x^2=(\sqrt{a^2+b^2})^2+c^2$
$a^2+b^2+c^2=x^2$
$x=\sqrt{a^2+b^2+c^2}$
Triángulo de Pascal
1.1.2 Denótese por $S_n,0,S_n,1,S_n,2$ a la suma de cada tercer elemento en el n-ésimo renglón del triángulo de Pascal, comenzando por la izquierda con el primer elemento, el segundo elemento, y el tercer elemento respectivamente. Haga una conjetura sobre el valor de $S_100,1$
Conjetura
La suma $S_100,1$ es la suma de los números triangulares que son de la forma $\frac{n(n+1)}{2}$ que aparecen en el triángulo en la tercera y antepenúltima diagonal por lo tanto $S_100,1$ será 5050 mas todos los números de la forma $\frac{n(n+1)}{2}$
Conjetura
La suma $S_100,1$ es la suma de los números triangulares que son de la forma $\frac{n(n+1)}{2}$ que aparecen en el triángulo en la tercera y antepenúltima diagonal por lo tanto $S_100,1$ será 5050 mas todos los números de la forma $\frac{n(n+1)}{2}$
Rapidez de variación
20. Problema de rapidez de variación. Se vierte agua en un recipiente de forma cónica con una rapidez r. El recipiente en forma de cono de base horizontal tiene el vértice dirigido hacia abajo; el radio de la base del cono es a, su altura b. Determine la velocidad a la que la superficie del agua se eleva cuando la profundidad del agua es y. Después, obtener el valor numérico de la incógnita, suponiendo que $a = 4 dm$, $b = 3 dm$, $r = 2 dm^3$ por minuto y $y = 1 dm$.
Para poder analizar y entender el problema hice una representación gráfica, con los datos proporcionados en dicho problema.
SOLUCIÓN:
Datos
El radio de la base del cono, a = 4 dm.
Altura del cono, b = 3 dm
Rapidez con que el agua se vierte en el recipiente r = 2 dm³ por minuto.
Profundidad del agua en un cierto momento, y = 1 dm.
Se supone que los alumnos conocen las reglas más elementales de diferenciación y la noción de ``rapidez de variación.''
- ¿Cuáles son los datos?
- El radio de la base del cono, a = 4 dm; la altura del cono, b = 3 dm, la rapidez con que el agua se vierte en el recipiente r = 2 dm³ por minuto, y la profundidad del agua en un cierto momento, y = 1 dm.
Ver figura abajo.
- Exacto. El enunciado del problema parece sugerir que se deben dejar de lado, provisionalmente, los valores numéricos y razonar con las letras, expresando la incógnita en función de a, b, r y y, y al final solamente, tras de obtener la expresión algebraica de la incógnita, sustituir los valores numéricos. Adoptemos esta sugerencia. ¿Cuál es la incógnita?
- La velocidad a la que se eleva la superficie del agua cuando la profundidad es y.
- Es decir,¿puede usted expresarlo en otros términos?
- La velocidad con que aumenta la profundidad del agua.
- Nuevamente, ¿puede usted enunciar el problema en forma diferente?
- La rapidez de variación de la profundidad del agua.
- Exacto: la rapidez de variación de y. Pero, ¿qué es la rapidez de variación? Considere usted la definición.
- La derivada de una función representa la rapidez de variación.
- Correcto. Ahora bien, ¿y es una función? Como ya lo hemos dicho, no nos ocuparemos de su valor numérico. ¿Puede imaginar que y varía?
- Sí, y, la profundidad del agua, aumenta a medida que pasa el tiempo.
- Por lo tanto, ¿ y es función de qué?
- Del tiempo t.
- Bien. Introduzca una notación apropiada. ¿Cómo expresaría usted ``la rapidez de variación de y''por medio de símbolos matemáticos?
- $\frac{dy}{dt}$
- Bien. He ahí pues su incógnita. Le hace falta expresarla en términos de a, b, r, y y. De hecho uno de estos datos es una rapidez de variación:¿cuál de ellos?
- r, que representa la rapidez de agua que cae en el recipiente durante un tiempo dado.
- ¿Puede decirlo en otra forma?
- r es la rapidez de variación del volumen de agua en el recipiente.
- Es decir, ¿puede enunciarlo nuevamente en forma diferente: ¿cómo podría escribirlo con una notación apropiada?
- $r = \frac{dV}{dt}$
- ¿Qué es V?
- El volumen de agua que hay en el recipiente en el instante t.
- Bien. Así pues, tiene que expresar $\frac{dy}{dt}$ en términos de a,b,$\frac {dV} { dt } $ , y.
¿Cómo va usted a tratar de hacerlo?
- ...
- Si no puede resolver el problema, trate de resolver, primero un problema relacionado. Si no ve la relación entre $\frac{dy}{dt}$ y los datos, trate de que aparezca alguna relación más sencilla que podría servirle de punto de partida.
_ ...
- ¿No ve usted que existen otras relaciones? Por ejemplo, ¿y y V son independientes una de otra?
- No. Cuando y aumenta, V debe aumentar también.
- Así hay una relación. ¿Cuál es, pues?
- Pues que V es el volumen del cono cuya altura es y. Pero desconozco el radio de la base.
- Sin embargo, puede tenerlo en cuenta. Déle un nombre cualquiera, x por ejemplo.
- $V = \frac{\pi x^2y}{3}$
- Exacto. Ahora, ¿qué sabe usted de x?¿Es independiente de y?
- No. Cuando la profundidad del agua, y, aumenta, el radio de la superficie variable x aumenta también.
- Así pues, hay una relación. ¿Cuál es ésta?
- Sí, claro, hay triángulos semejantes:
$x : y = a : b$
- Una relación más, ¿ve usted? No hay que desaprovecharla. No olvide que usted quería conocer la relación existente entre V y y.
- Se tiene
$x = \frac{ay}{b}$
$V = \frac{\pi a^2y^3}{3b^2}$
- Muy bien. Esto me parece un buen punto de partida. ¿Qué le parece a usted? Pero no olvide su propósito. ¿Cuál es la incógnita?
- $\frac{dy}{dt}$
- Tiene que encontrar una relación entre $\frac{dy}{dt}$, $\frac{dV}{dt}$ y otras cantidades
- Aquí tiene una entre y, V y otras cantidades. ¿Qué hacer?
- Pues claro, diferenciando se tiene
$\frac{dV}{dt} = \frac{\pi a^2y^2}{b^2}\cdot\frac{dy}{dt}$
He ahí la solución.
-Perfecto. Y, ¿para los valores numéricos?
- Si a = 4, b = 3, $\frac{dV}{dt} = r =$ 2, y = 1, entonces
$2 = \frac{\pi \times 16 \times 1}{9}\cdot \frac{dy}{dt}$.
¿para los valores numéricos?
Si $a = 4$, $b = 3$, 2, $y = 1$, entonces
El resultado numérico es:
$\frac{dy}{dt}=\0.358098622$
Para poder analizar y entender el problema hice una representación gráfica, con los datos proporcionados en dicho problema.
SOLUCIÓN:
Datos
El radio de la base del cono, a = 4 dm.
Altura del cono, b = 3 dm
Rapidez con que el agua se vierte en el recipiente r = 2 dm³ por minuto.
Profundidad del agua en un cierto momento, y = 1 dm.
Se supone que los alumnos conocen las reglas más elementales de diferenciación y la noción de ``rapidez de variación.''
- ¿Cuáles son los datos?
- El radio de la base del cono, a = 4 dm; la altura del cono, b = 3 dm, la rapidez con que el agua se vierte en el recipiente r = 2 dm³ por minuto, y la profundidad del agua en un cierto momento, y = 1 dm.
Ver figura abajo.
- Exacto. El enunciado del problema parece sugerir que se deben dejar de lado, provisionalmente, los valores numéricos y razonar con las letras, expresando la incógnita en función de a, b, r y y, y al final solamente, tras de obtener la expresión algebraica de la incógnita, sustituir los valores numéricos. Adoptemos esta sugerencia. ¿Cuál es la incógnita?
- La velocidad a la que se eleva la superficie del agua cuando la profundidad es y.
- Es decir,¿puede usted expresarlo en otros términos?
- La velocidad con que aumenta la profundidad del agua.
- Nuevamente, ¿puede usted enunciar el problema en forma diferente?
- La rapidez de variación de la profundidad del agua.
- Exacto: la rapidez de variación de y. Pero, ¿qué es la rapidez de variación? Considere usted la definición.
- La derivada de una función representa la rapidez de variación.
- Correcto. Ahora bien, ¿y es una función? Como ya lo hemos dicho, no nos ocuparemos de su valor numérico. ¿Puede imaginar que y varía?
- Sí, y, la profundidad del agua, aumenta a medida que pasa el tiempo.
- Por lo tanto, ¿ y es función de qué?
- Del tiempo t.
- Bien. Introduzca una notación apropiada. ¿Cómo expresaría usted ``la rapidez de variación de y''por medio de símbolos matemáticos?
- $\frac{dy}{dt}$
- Bien. He ahí pues su incógnita. Le hace falta expresarla en términos de a, b, r, y y. De hecho uno de estos datos es una rapidez de variación:¿cuál de ellos?
- r, que representa la rapidez de agua que cae en el recipiente durante un tiempo dado.
- ¿Puede decirlo en otra forma?
- r es la rapidez de variación del volumen de agua en el recipiente.
- Es decir, ¿puede enunciarlo nuevamente en forma diferente: ¿cómo podría escribirlo con una notación apropiada?
- $r = \frac{dV}{dt}$
- ¿Qué es V?
- El volumen de agua que hay en el recipiente en el instante t.
- Bien. Así pues, tiene que expresar $\frac{dy}{dt}$ en términos de a,b,$\frac {dV} { dt } $ , y.
¿Cómo va usted a tratar de hacerlo?
- ...
- Si no puede resolver el problema, trate de resolver, primero un problema relacionado. Si no ve la relación entre $\frac{dy}{dt}$ y los datos, trate de que aparezca alguna relación más sencilla que podría servirle de punto de partida.
_ ...
- ¿No ve usted que existen otras relaciones? Por ejemplo, ¿y y V son independientes una de otra?
- No. Cuando y aumenta, V debe aumentar también.
- Así hay una relación. ¿Cuál es, pues?
- Pues que V es el volumen del cono cuya altura es y. Pero desconozco el radio de la base.
- Sin embargo, puede tenerlo en cuenta. Déle un nombre cualquiera, x por ejemplo.
- $V = \frac{\pi x^2y}{3}$
- Exacto. Ahora, ¿qué sabe usted de x?¿Es independiente de y?
- No. Cuando la profundidad del agua, y, aumenta, el radio de la superficie variable x aumenta también.
- Así pues, hay una relación. ¿Cuál es ésta?
- Sí, claro, hay triángulos semejantes:
$x : y = a : b$
- Una relación más, ¿ve usted? No hay que desaprovecharla. No olvide que usted quería conocer la relación existente entre V y y.
- Se tiene
$x = \frac{ay}{b}$
$V = \frac{\pi a^2y^3}{3b^2}$
- Muy bien. Esto me parece un buen punto de partida. ¿Qué le parece a usted? Pero no olvide su propósito. ¿Cuál es la incógnita?
- $\frac{dy}{dt}$
- Tiene que encontrar una relación entre $\frac{dy}{dt}$, $\frac{dV}{dt}$ y otras cantidades
- Aquí tiene una entre y, V y otras cantidades. ¿Qué hacer?
- Pues claro, diferenciando se tiene
$\frac{dV}{dt} = \frac{\pi a^2y^2}{b^2}\cdot\frac{dy}{dt}$
He ahí la solución.
-Perfecto. Y, ¿para los valores numéricos?
- Si a = 4, b = 3, $\frac{dV}{dt} = r =$ 2, y = 1, entonces
$2 = \frac{\pi \times 16 \times 1}{9}\cdot \frac{dy}{dt}$.
¿para los valores numéricos?
Si $a = 4$, $b = 3$, 2, $y = 1$, entonces
El resultado numérico es:
$\frac{dy}{dt}=\0.358098622$
lunes, 11 de octubre de 2010
domingo, 26 de septiembre de 2010
Cubo de Rubik
Yo nunca he jugado el cubo de Rubik utilizando algún método, solo lo intente una vez con unos amigos de la uam y tuve la suerte de poder resolverlo haciendo pocos movimientos.
Clase del 22 de Septiembre del 2010
SUDOKU
Estos fueron algunos consejos que encontré en Internet para resolver sudokus :- Empieza utilizando un método de eliminación
- Al eliminar números, recuerda usar también las regiones cuadradas
- Empieza por los Sodokus de nivel muy fácil o fácil.
- Una vez que hayas terminado, haz un repaso rápido para comprobar que todo está bien.
El maestro Cantoral nos dejo de tarea resolver un Sudoku pueden verlo Aqui
Clase del 21 de septiembre del 2010
Número de subconjuntos de un conjunto
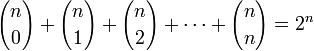
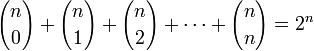
Tarea 1. Demostrar para n=3
$2^3=8$
{ } {1} {2} {3} {123} {12} {32} {31}
Clase del 20 de septiembre del 2010
En esta clase resolvimos algunos problemas de Física, utilizando los pasos de Polya Matemático de Budapest Hungría (13 de diciembre de 1887 – 7 de septiembre de 1985) para la resolución de problemas.- Entender
- Estrategia
- Ejecución
- Revisar
Además del método de Polya me parece interesante el método que utilizó otro físico matemático llamado Henri Poincaré, jugando un papel crucial el subconsciente. Llamaba a la primera etapa "preparación" , a la segunda "incubación seguida de la iluminación", y a la tercera "verificación".
Adoquinado de Penrose
Consiste en cubrir cualquier superficie con un patrón de dos figuras que forman un módulo no periódico e infinito.Este es el mosaico que se encuentra el el museo Uiversum
Suscribirse a:
Entradas (Atom)